HOME CONTACT SUPPORT SENSORYTEST.COM | |||
|
|
HOME CONTACT SUPPORT SENSORYTEST.COM |
|
Sensory testing professional's favorite virtual desktop. Say hello to SIMS Cloud Systems. From any device, any laptop, any iPad and even your cell phone. Log in from anywhere anytime. Inquire today. 
|
Mobile devices real test example Point your cell phone camera Easy for your respondents 
Link |
VIEW REPORTS |
QUESTION CHOICES |
TEST CHOICES |
View More Question Type Choices |
| MAXDIFF EXAMPLES |
|
MAXDIFF Most Important & Least Important scaling MAXDIFF Best & Worst scaling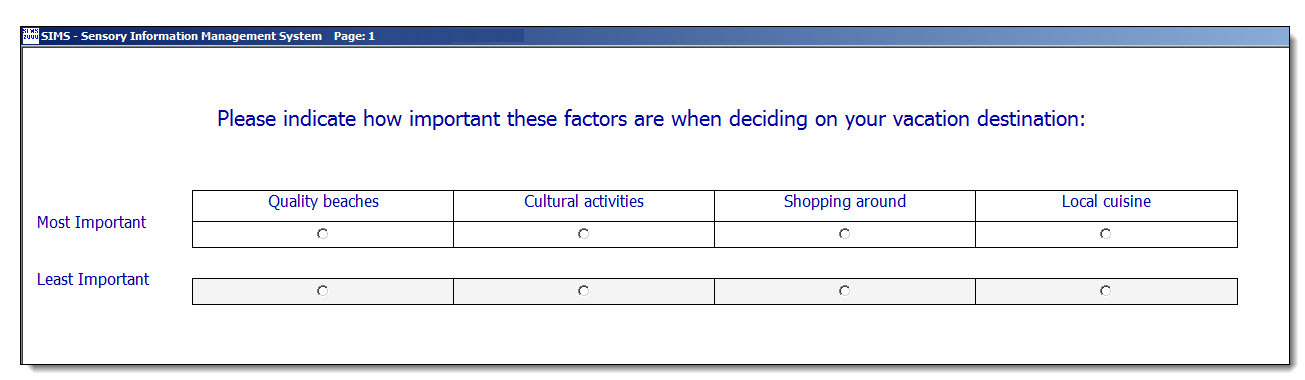 
(The scales on this Web page are not interactive.) SIMS software express package file: MAXDIFF.SIMS2000ExpressPackage.sql.ZIP Ballot Setup Vacation Destination example type question, Xlstat. Design 8C4, unbalanced incomplete block design. Ballot branching to force only one presentation.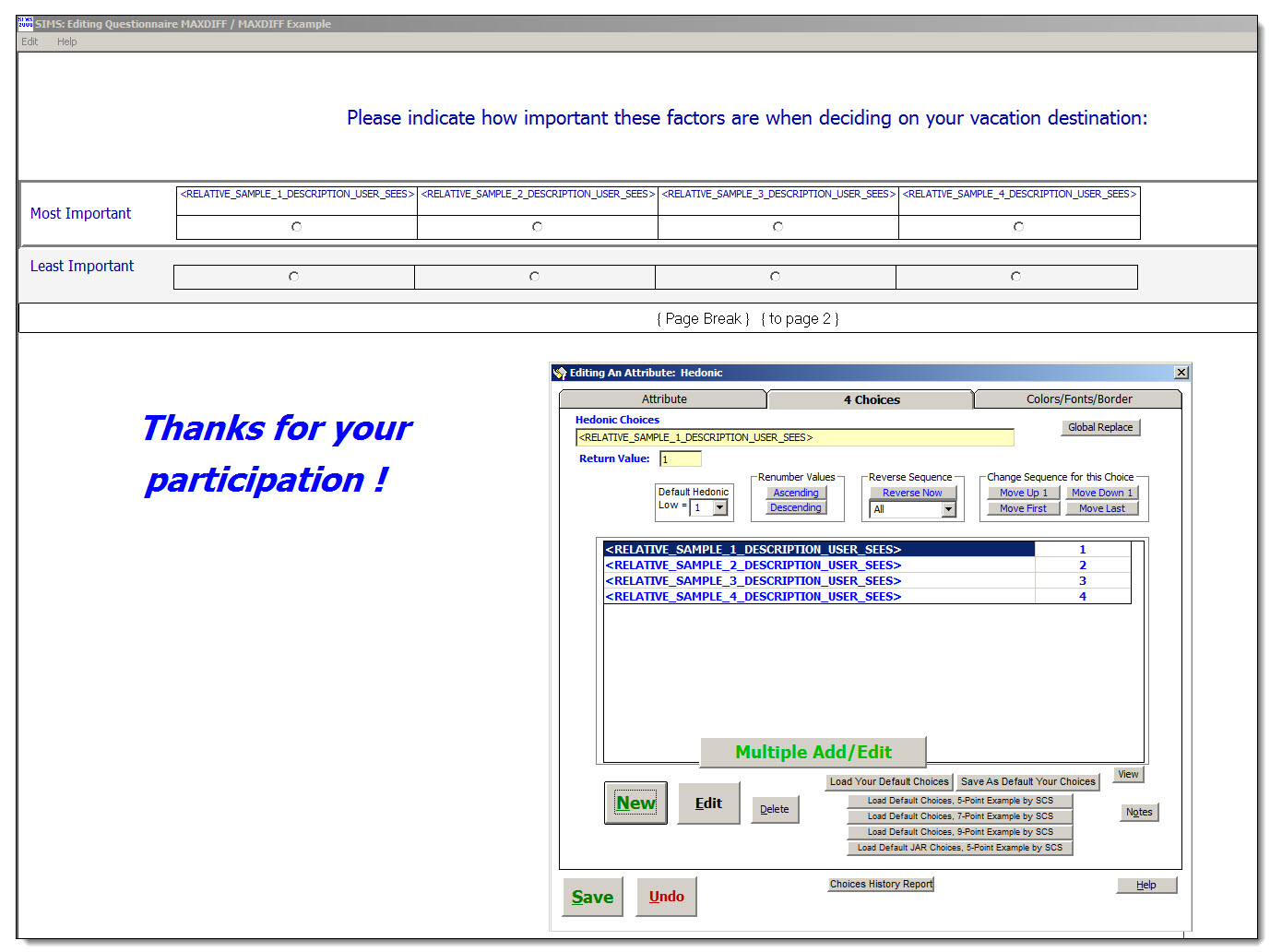 
Experimental Design Setup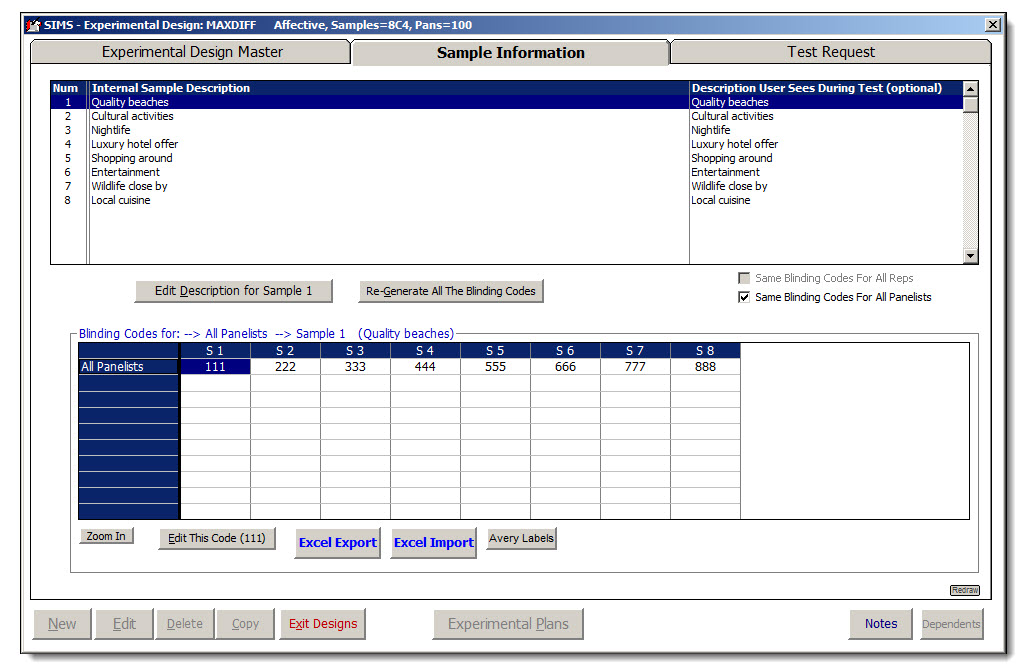 
Report Raw Data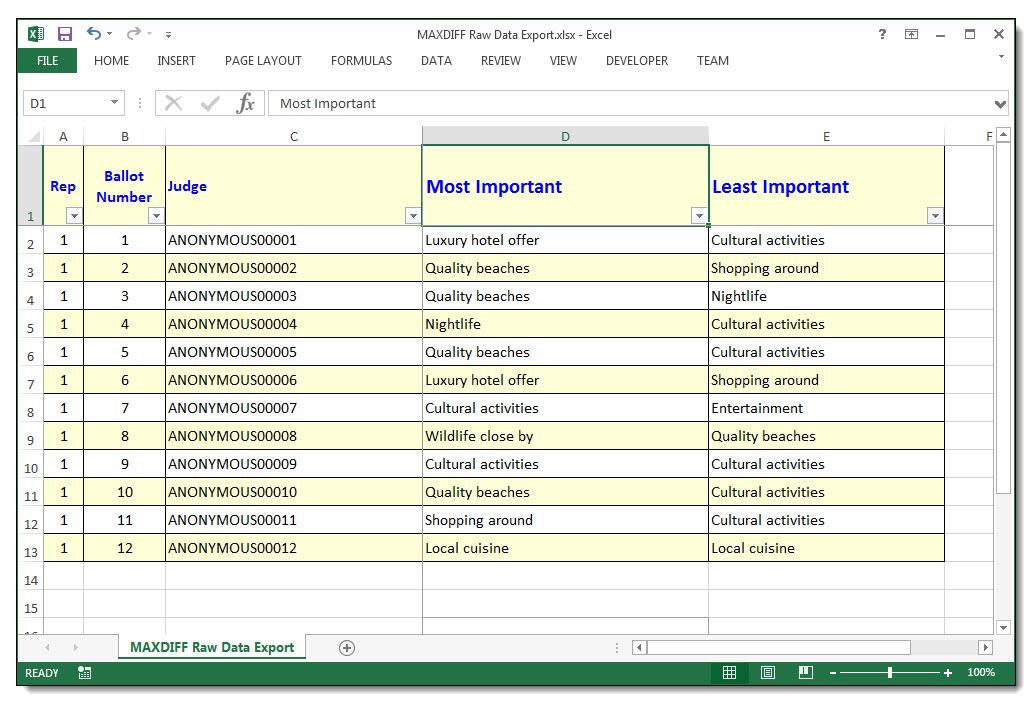 
SIMS software express package file: MAXDIFF.SIMS2000ExpressPackage.sql.ZIP There's no MaxDiff analysis built into SIMS as of yet. Here are some MaxDiff data analysis helpful links. MaxDiff Analysis References: XLStat Analysis: XLStat Data analysis with a specific method: hierarchical bayes. SAS Analysis: MktMDiff (PDF) Process Google: www.google.com/search?q=maxdiff+xlstat Wikipedia: Wikipedia Notes: Yes you can use SIMS for MAXDIFF ballots/designs. Analysis is a la cart via XLStat, SAS, or any method of your choosing. It's all about your SIMS Experimental Design. "Sampling" the Attributes/Concepts, where the Attributes become the Experimental Design's samples. Ballots: Subjects will choose the Most Important and Least Important from BIBD set of Attributes/Concepts presented. At least 2 hedonic questions. Which is Most Important? Which is Least Importan? Use special Hedonic Choice tags <RELATIVE_SAMPLE_[1]_BLINDING_CODE> in both questions. Experimental Designs: An experimental design for a MaxDiff study is a block design. A set of t attributes are organized into b blocks or sets of size k. Ideally, it's preferred to use a balanced incomplete block design or BIBD. In a BIBD, each of the t attributes appears the same number of times, and each of the t attributes appears with every other attribute the same number of times. However, BIBDs do not exist for every combination of b, t, and k that might be of interest. Hence, in many situations use unbalanced block designs in which each of the t attributes appears the same number of times, but not all of the t(t ? 1)/2 pairs of attributes appear the same number of times. Fortunately, while a BIBD is nice, it is not required for a MaxDiff analysis. |
